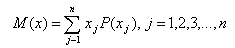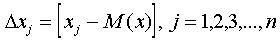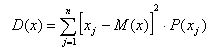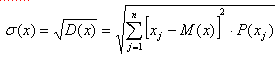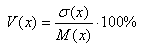Оценка риска в расчетах цен

Методы оценки риска в расчетах цен. Риск в предпринимательстве – это вероятность возникновения убытков или каких-либо потерь в результате не осуществления намечавшегося события, предусмотренного прогнозом, планом, проектом, программой. Поэтому в более или менее сложных ситуациях, требующих крупных затрат для оценки степени риска в мероприятиях, намечаемых руководством предприятия, целесообразно привлекать математиков-специалистов, знакомых с теорией вероятностей и математической статистикой.

Вероятность события определяется как мера, число, показывающее отношение числа благоприятствующих этому событию исходов к общему числу всех единственно возможных и равновозможных элементарных исходов в системе намечаемых мероприятий.

Вероятность достоверного события равна единице, невозможного события – нулю. Вероятность случайного события есть положительное число, заключенное между нулем и единицей. В статистических исследованиях вероятность будущего события исчисляется как относительная частота наступившего события, т.е. отношение числа испытаний, в котором данное событие появилось, к общему числу фактически проведенных испытаний. Проще говоря, вероятность означает возможность получения определенного результата. Если вы определили цену единицы товара в размере 100 рублей, то в случае, когда у вас 80% этого товара реализуется по этой цене, вероятность правильности определения цены равна 0,8, а риск за ошибку составит 0,2 или 20%.

Так как риск в бизнесе связан с вероятностью не осуществления вашего мероприятия, с просчетами или недоучетом реальных событий в хозяйственной жизни, то это – противоположное событие по отношению к реализуемому вами мероприятию.

Противоположное событие – это событие, вероятность которого по отношению к исходному событию является разностью между единицей и вероятностью осуществления исходного события, т. е. намеченного и реализуемого мероприятия. В расчетах цены приходится использовать методы оценки вероятности как исходного события – подтверждения правильности расчета цены (тогда риск равен вероятности ее ошибки, т.е. 1±Р(р), где Р(р) – вероятность того, что цена будет находиться в расчетном интервале), так и оценки вероятности ее отклонения от расчетной (оценки степени риска).

Рыночная цена по своей природе является случайной величиной, которая в условиях конъюнктуры рынка вследствие сделки купли-продажи примет одно и только одно возможное значение, наперед точно не известное и зависящее от многих случайных причин, которые заранее не могут быть все учтены участниками сделки (кроме, может быть, тех, которые предусмотрены ранее заключенными договорами). Случайная величина – это переменная величина, конкретное значение которой не определено, зависит от случая, но для которой определена функция распределения вероятностей. Последняя и позволяет судить о степени риска.

В условиях ограниченной информации при расчетах цен большей частью бывает трудно подобрать достаточно подходящую эмпирическую функцию распределения вероятностей. Поэтому в практических расчетах, по-видимому, удобнее пользоваться наиболее часто употребляемыми в теории вероятностей стандартными функциями распределения вероятностей, в частности:

- нормальным распределением вероятностей, или распределением Гаусса;
- показательным (экспоненциальным) распределением вероятностей, которое весьма широко используется в расчетах надежности. Расчет экономических показателей, в том числе и цен, требует определенных критериев надежности;
- распределением Пауссона, которое часто используется в теории массового обслуживания.

Практика расчетов может подсказать и другие, в частности эмпирические, распределения вероятностей.

Ценовая информация, особенно в современных условиях, требует постоянного пополнения и обработки применительно к новым условиям. Для анализа рисковых показателей она нуждается в статистической обработке. Между тем ее большей частью бывает недостаточно. Поэтому приходится пользоваться экспертными оценками. Отсюда информацию по определению риска следует условно разделить на два вида:

1. объективную, или статистическую, информацию, которая может быть использована для расчета вероятностных характеристик оценки риска;
2. субъективные экспертные оценки, которые являются предложениями экспертов, специалистов. Нередко интуитивные, они могут способствовать выработке наиболее удачного решения.

Вероятностная оценка риска математически отработана, имеет свои теоремы и методы исчисления, но довольствоваться этим в предпринимательской деятельности тоже весьма рискованно, потому что реальная точность математического расчета во многом зависит от исходной информации. Поэтому и здесь нельзя отказываться от предпринимательской интуиции.

В оценке предпринимательского риска используются перечисленные ниже характеристики.

Математическое ожидание значения экономического показателя, обусловленного неопределенностью ситуации, обычно определяется как средневзвешенное по вероятности возможных его значений, где вероятность каждого значения используется в качестве удельных весов, или статистической частоты. Математическое ожидание исчисляется по следующей формуле:

где,
М (х) - математическое ожидание случайной (дискретной) величины. Через х в данном разделе обозначается любая случайная величина, будь то цена дохода, прибыль и т.д.;
хj - значение случайной величины в частном случае, т.е. на рассматриваемом сегменте рынка реализации конкретного товара, или применительно к разным предприятиям и т.д.; Р(хj) - вероятность случайной величины х; n – общее число вариаций случайной величины х.

Абсолютное отклонение возможных случайных значений экономического показателя от математического ожидания этого показателя, т.е. его средневзвешенного по вероятности значения, характеризует амплитуду изменчивости этого показателя. Часто имеет смысл рассчитать максимальное абсолютное отклонение, а иногда и наименьшее абсолютное отклонение. При реализации товара на различных рынках или различным заказчикам полезно сопоставить абсолютное отклонение цены от ее среднего уровня. Большие абсолютные отклонения настраивают на возможность риска. Однако экстремальные исключительные отклонения при реализации товара отдельным заказчикам могут быть локализованы общей стратегией маркетинговой политики. Поэтому требуются более общие показатели оценки риска.

Абсолютные отклонения определяются по формуле:

где Δxj – абсолютное отклонение случайного значения величины от математического отклонения М(х).

Дисперсия дает более общую оценку отклонений и представляет собой средневзвешенное квадратов отклонений конкретных показателей (вариаций) от математического ожидания, т.е. среднего ожидаемого его значения. Дисперсия исчисляется по формуле:

где D(x) – дисперсия случайной величины х.

Среднее квадратическое отклонение, или стандартное отклонение, представляет собой квадратный корень из дисперсии. Эта вероятностная, статистическая характеристика больше приближается к интуитивным представлениям об оценке изменчивости конъюнктуры рынка, ценностных показателей, поскольку сопоставления ведутся уже не с квадратами отклонений, а с квадратным корнем из суммы квадратных отклонений. Иначе говоря, вероятностные отклонения приводятся в реальную размерность. Среднее квадратическое отклонение вычисляется по формуле:

где D(x) – традиционное обозначение среднего квадратического отклонения, или стандартного отклонения, случайной величины х.

Коэффициент вариации случайной величины V(x), представляющий собой выраженное в процентах отношение среднего квадратического отклонения к математическому ожиданию, или средневзвешенному значению этой величины:

Практическое значение перечисленных характеристик состоит прежде всего в том, что они позволяют весьма осмысленно подойти к количественной оценке предпринимательского риска. На практике к тому же часто бывает трудно определить закон распределения случайной величины. Приходится довольствоваться гипотезой, условным допущением. В этих случаях бывает достаточно знать числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение, коэффициент вариации.

Математическое ожидание М(х) применяется для усреднения исследуемых величин, цен, которые зависят от случайных условий, когда информация имеет известный разброс. С математическим ожиданием обычно связывают точку, в окрестности которой вероятность имеет наибольшее значение. Поэтому в экономических расчетах часто используются показатели средних цен, индексы средних цен, средней себестоимости, средней рентабельности, поскольку конкретные цены даже в пределах одного рынка имеют, как правило, некоторый разброс.

Абсолютные отклонения Δxj показывают абсолютные размеры разброса значений исследуемой величины. При этом полезно знать максимальные значения абсолютных отклонений в положительном и отрицательном направлениях. Известную информацию дает также размах варьирования, размеры отклонений конкретных цен от их среднего значения.

Размах варьирования (отклонений) представляет собой разность между наибольшим и наименьшим значениями исследуемой величины:

R = x_max – x_min

При анализе рядов цен за какой-то период следует учитывать, что максимальные и минимальные отклонения могут быть вызваны какими-либо особыми факторами, например резким изменением цен на основное сырье, исходные материалы.

Дисперсия D(x), давая общую характеристику квадратов отклонений случайной величины, позволяет, во-первых, устранить различия в положительных и отрицательных отклонениях, так как квадрат отрицательной величины является положительной величиной; во-вторых, при ее исчислении усиливается значение больших отклонений и уменьшается значение малых отклонений. Это соответствует закономерности квадратичной функции.

Среднее квадратическое отклонение исчисляется, в отличие от дисперсии, в той же размерности, что и сама случайная величина. Может, именно это послужило причиной его широкого применения для характеристики отклонений и вероятностей оценки поведения случайной величины. В частности, среднее квадратическое отклонение имеет чрезвычайно важное значение для критериальной характеристики так называемого принципа практической уверенности.

В ценообразовании это может быть вывод о возможных отклонениях цены от принятой в расчетах, отклонениях спроса при изменении цены, отклонениях возможных доходов, прибыли.

Среднее квадратическое отклонение позволяет определить количественные интервалы принципа практической уверенности в виде «правила трех сигм»: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

Таким образом, зная среднее квадратическое отклонение, можно с достаточной практической уверенностью сказать, что все рассеивание данной случайной величины укладывается в интервал М(x)±3σ(x). Вероятность того, что значение случайной величины будет находиться в этом интервале при нормальном распределении, равна 0,9973. Вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала – 0,0027. Это может произойти лишь в 0,27% случаев.

Принцип разумной уверенности, или разумного риска, в предпринимательской деятельности означает, что в принятии решения руководствуются таким соотношением вероятностей осуществления и неосуществления события, при котором примерно две трети шансов благоприятствуют успеху и одна треть шансов ему не благоприятствует («Правило 70/30»).

Неблагоприятная одна треть шансов является стимулятором для рассмотрения и принятия мер по их предотвращению.

Этому правилу при нормальном распределении соответствует интервал значений случайной величины, равный отклонению от математического ожидания в пределах среднего квадратического отклонения, т.е. М(х) + (х). Для экономиста часто бывает привычнее пользоваться для характеристики отклонения процентными соотношениями.

Коэффициент вариации при нормальном распределении вероятностей характеризует интервал отклонения случайной величины при вероятностном исходе, соответствующем двум третям шансов «за» и одной трети шансов «против» в процентном отношении (привычном для экономиста) к математическому ожиданию. Поэтому можно считать, что коэффициентом вариации в ценностных расчетах целесообразно и необходимо пользоваться. Он дает определенную (хотя и вероятностную) базу для ценностных расчетов.